
ーーーーーーーーーーーーーーーーーー
・子どもがわり算苦手!どうしたらよいの?
・子どもにわり算を教える教え方を知りたい
・わり算が嫌いにならないように教えてあげたい
ーーーーーーーーーーーーーーーーーー
こんな悩みを解決できる記事を用意しました!
この記事で紹介する「わり算の教え方」を実践すれば、わり算が難しいと思っている子どもがわり算は簡単と思えるようになります。
また、自分の子がわり算苦手と言っている理由がわかり、子どもがわからないことに「なんでわからないの!!もー」とイライラすることが減ります。
今回ご紹介する「わり算の教え方」は長年そろばん教室で指導を行なっている私が実際に指導を行い、たくさんの子ども達と接し解決してきた内容です。
記事前半では、なぜわり算は難しいのか・わり算学習の価値について、後半ではわり算の教え方を解説するので、ぜひ参考にしてくださいね!
※「すぐにわり算の教え方について知りたい!」という方は、「わり算教え方のポイント」へどうぞ!
「このページの内容の概要は動画でもご覧頂けます」
動画での解説は、概要です。
詳細まで知りたい方は、このページの最後までお読みください。
わり算はなぜ難しいのか?

「わり算」は小学3年生の4月頃に学習する科目です。
2年生の年末に、かけ算九九を覚え、学年が上がってすぐにわり算の学習がスタートします。
かけ算九九を理解しているにも関わらず、わり算が苦手な子どもは多いです。
「子どもはかけ算できるのに、わり算が苦手でどうしたらよいの…」と
心配しているお母さん方に少しでもお役に立てるように、
☆わり算はどうして難しく感じるのか
☆わり算をしっかり身につける重要性
☆わり算の教え方のポイント(基礎編)
をお伝えします。
量が多い

わり算が難しく感じてしまう理由は、かけ算に比べて組み合わせの量が多いためです。
かけ算の素過程(それ以上小さくできない値)は、0×0、9×9など1位数と1位数のかけ算は100通り
それに比べて、
わり算の素過程は、あまりのある場合も含めて、0÷1、6÷3、7÷3、89÷9など1位数や2位数を1位数でわって答えが1位数のわり算は450通りあります。
かけ算と比べると4.5倍の量になります。
例えば、100個のボールから1個のボールを探すのと
450個のボールから1個を探すのを比べたら、かなり大変に感じませんか?
それと同じで、計算のパターンの数が多くなるとその分難しくなります。
すべて使っての計算

わり算の計算は、数をたてて→かけて→ひいての順に答えをだします。
たし算の考えを使いつつ、かけ算、ひき算とすべて使って計算するため複雑です。
途中でなに算をやっているのか迷う子もいます。
例えば、普通に歩くだけだったら難しくないけど、
普通に歩いていて、次はスキップして、次はダッシュしてといろいろなことを要求されたら難しいし疲れませんか?
すべて使ってやるって複雑です。
それぞれのたし算、ひき算、かけ算の意味を理解していないと難しく感じます。
計算順番が逆
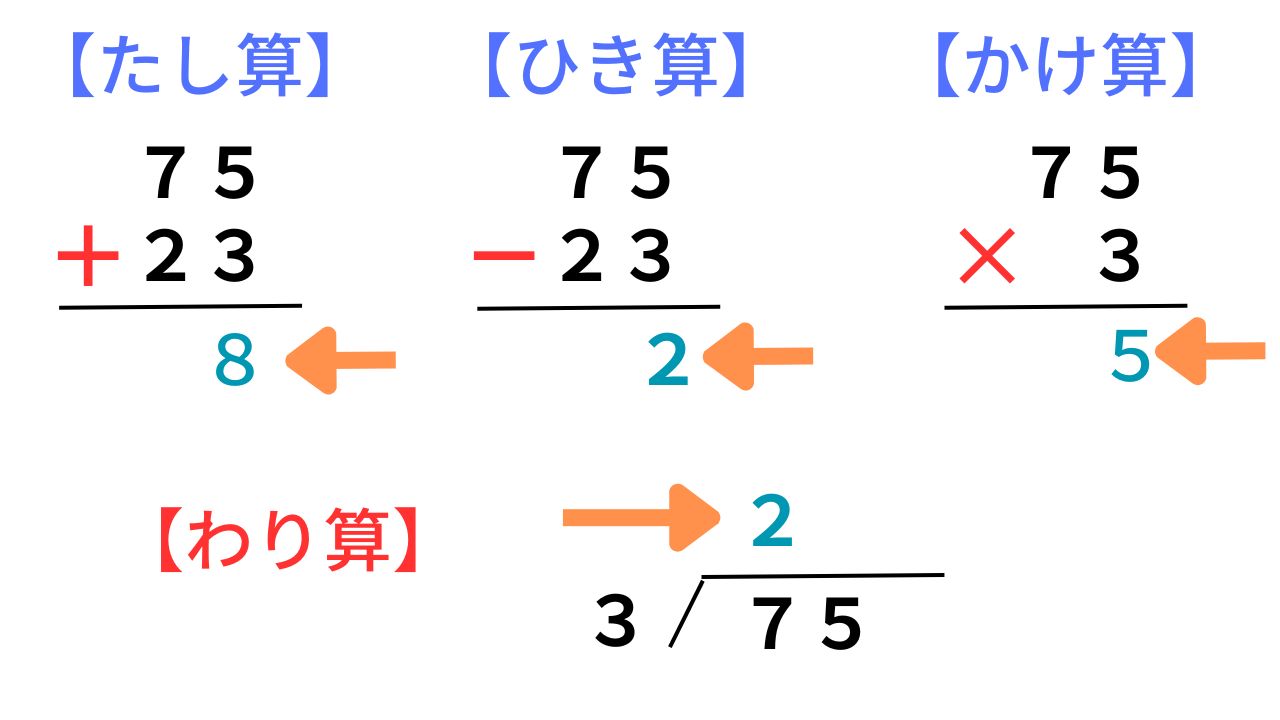
わり算は、今まで習ってきたたし算、ひき算、かけ算と違って、計算の順番が逆になります。
筆算で考えると、
たし算、ひき算は1の位から計算します。
例えば、「75 + 23」、「75−23」上記絵のように、右から計算していきます。
かけ算も1の位からかけていくため、
例えば、「75×3」も上記図のように、右からの計算になります。
わり算を習うまでの計算は、筆算でいうと右から計算。
それに対して、わり算は、左から(大きな位)の計算になります。
例えば、「75÷3」の筆算は上記の図のように、左からですよね。
このように、わり算は計算する順番が逆になり、戸惑い難しいって感じてしまいます。
あまりがある

わり算の難しさにあまりの問題があります。
あまりの計算があるおかげで、先ほどお伝えした組み合わせの量がかけ算より多くなっています。
わりきれる問題であれば、九九を覚えることで簡単に答えがだせそうですが、
わりきれない計算が何通りもあるおかげで、答えを出すのが難しく感じます。
しかし、あまりのある計算はとても大事です。
日常生活でも物を人数分にわける時ってだいたいあまりがでますよね。
あれ、1こあまった~じゃんけんで誰が食べるか決めようかー
よくわが家でもバトルになります。
あまりのある計算、日常にも使いますし、2桁3桁と大きい数の計算になった時、
あまりのある計算を使って順序良く計算するのがほとんどです。
難しく感じるけど、あまりのあるわり算はしっかり理解することが大事です。
意味が2通り

わり算には2つの意味があります。
ここまでわり算の難しい部分をお伝えしましたが、これが一番難しい理由です。
文章問題を理解するのに、ここが子どもたちの一番迷うところになります。
わり算の2つの意味とは
「等分除(とうぶんじょ)」と「包含除(ほうがんじょ)」のことです。
わり算は「わける」ことですが、わけるにも意味がわかれています。
分けられる数のところまで分けていく、同じ数に分けるということです。
「等分除」→分けられる数のところまで分けていく1あたりの数を求める
「全体の数÷いくつ分=1あたりの数」
つまり、例でお伝えすると、
Q、クッキーが12こあります。3人で同じ数ずつ分けると、1人分は何こになりますか。(東京書籍 新しい算数3年生上巻教科書引用)
上記絵のように、分けられる数まで分けていきながら、1人あたりの数を求める問題です。
「包含除」→同じ数に分けるいくつ分をもとめるわり算
「全体の数÷1あたりの数=いくつ分」
こちらも、例でお伝えすると、
Q、パイが12こあります。1人に3こずつ分けると、何人に分けられますか。
(東京書籍 新しい算数3年生上巻教科書引用)
下記絵のように、同じ数を何人に分けられるかの数を求める問題です。
同じわり算でも求める意味が違い、答えも違います。
3年生の教科書は、先に「等分除」を教えてからすぐに「包含除」を教えます。
その後は2つの意味の問題がランダムに出題されます。そのため何を聞かれている問題かが整理できず難しく感じてしまう子が多いです。
計算ドリルのように式の答えだけだす問題であれば、意味は考えなくても計算のやり方さえ覚えれば答えられます。子どもも指導者もラクです。
しかし、この一番難しいわり算の意味を理解することなく、形だけ答えをだしていても、
日常で使える役立つわり算にはなりません。意味の理解とても大事です。
🍀 無料プレゼントのお知らせ
もし、
✔ うちの子がどの段階で止まっているのか知りたい
✔ 家庭で何から始めればいいか迷っている
✔ 割り算の“どの部分”が弱いのか知りたい
と思われたら、
🎁 無料診断チェックシート(PDF) 🎁 割り算教える順序動画(期間限定視聴)
をLINEで受け取れます。
✔ 3分でつまずき原因が分かる
✔ 家庭での次の指導がわかる
✔ 子どもが混乱しにくい教え方が分かる
👇 無料診断・順序動画を受け取る(登録30秒)
わり算はなぜ大事か?
分数・小数の土台になる
わり算はなぜ大事なのか、
それは今後算数で学んでいく小数、分数、単位の計算や量、割合につながり、中学や高校の数学にもわり算の土台が活用されるからです。
小数は、1÷10=0.1などわり算を元にして考えたり、
中学数学でも多く出題される分数は、小数と同様にわり算が土台となっています。
単位計算の速さ(m/分)などはわり算の意味をしっかり理解していないと迷ってしまいます。
まずは、簡単な数のわり算問題からしっかり意味づけ学習に取り組むことが大事です。
そこから幅広く数の知識が広がっていきます。
日常生活でよく使う

日常生活で、結構わり算使っていませんか?
お菓子を家族に配り分ける時、
お店に行くとバーゲン何パーセント引きのうれしい赤札が、いくら安くなっているかの計算もかけ算わり算を使います。
広告には、数字のマジックがあって1,000mg配合など、1,000と数が大きいからたくさん入っているんだろうなと思わせて、単位で計算するとあまり入っていない…など見破る計算もわり算を使用します。
数字のマジックに騙されないように、わり算を使いこなせることが大事なんです。
それには、わり算の基礎を教える時に、どんな場面でどんな計算をつかうのか意味を紐づけて教えることが大事です。
わり算教え方のポイント

わり算の教えるポイント
まずは、かけ算をしっかり理解させることです。
理解するとは、ただ単に九九が言えるようになれば良いものではありません。
「九九が言える」+「意味づけ」が大事です。
2年生の学校授業で、先生の九九テストで早く覚える必要性から、
呪文のように唱えたり、九九の歌を聴きながら覚えたり、いろいろなやり方で九九を覚えていきます。
学校での先生の九九テストは、いかに早く間違えないかを重視することが多いようです。
特にこの時期の低学年の子は、「早く言える」=カッコいいと思ってしまう子が結構多いのですが、その早くのスピードばかり意識すると、かけ算理解に必要な意味づけをおろそかになってしまうことがあります。
そうなると、間違っていることに気づかない。
言語の音で1度覚えてしまったものは、直すのに大変苦労します。
例えば、むかしの歌が町で流れていて歌ったら、その歌詞違うよと指摘されたけど、
しばらくしてまた間違ったままの歌詞で歌っていたってことないですか?
音声で覚えたものは、意味付づけがしっかりしていないと自分の間違いに気づけないばかりか、応用できるかけ算にはなりません。
この応用できるかけ算が、わり算ができるに繋がります。
応用できるかけ算は、スピード重視ではなく意味づけ重視で身につきます。
もちろん2の段を言うのに10秒以上かかってしまうのであれば別に練習は必要ですが、
先に意味づけをしっかり教えて、そこから徐々にスピードを上げていく順番が大事です。
それでは、かけ算の意味づけで大事なこと3つをご紹介します。
①同数累加(どうすうるいか)の仕組みを理解させる
②数式が音声と結びついていること
③倍概念をしっかりつける
です。
①同数累加(どうすうるいか)とは、同じ数(A)を何回(B)も加えることです。
A+A+A+A…の大きさを求める時に、かけ算「A×B」をつかいます。
その1番わかりやすい教え方が下記の絵のように、
(1)かけ算は、同じ数同士のたし算を簡単にする計算だと意味づけする
(2)かける数が1ずつ増えると、かけられる数ずつ増える(減るも同様)の理解
(3)分解を理解させる
(例)横に8この☆を書く→子どもに2この☆を〇でかこんでもらう→
〇でかこんだ下に2と書かせる→あわせるから2と2の間になんの記号がつくと聞き、+を書いてもらう→
2+2+2+2=8になる→〇の数いくつ分と聞く(4つ分)→それをかけ算にすると「2×4=8」を理解させる
2×2=4、2×3=6、2×4=8 の数式を書かせ、答えはいくつ増えているを聞く
2×4=2×1+2×3を理解させる
この仕組みをきちんと理解させて意味づけをすることが、2桁のかけ算の学習になった時に仕組みがわかり、わり算理解に繋がります。
②「にしがはち」という音声と「2×4=8」の数式が頭で一致していることが大事です。
例えば幼児で、小学生のお姉ちゃんが九九を言えているのを聞いて、「かっこいい~」自分も覚えたいとなる子がいます。
その子が数を理解していない段階で、音声だけで間違えて覚えてしまったら直すのが大変です。
歌の音声は覚えると無意識に歌ってしまいますよね。
先ほどもお伝えしたように、音声で覚えたものは修正がむずかしい。
幼児の場合は、数の量を理解し数字と量が一致してから、九九を覚えることがおすすめです。
小学生も九九を覚える時は、お風呂場などに貼ってある九九表を見ながらしっかり、数式と音声を一致させてから覚えることが大事です。
③倍概念をしっかりつける
倍概念は、系列で教えることで理解に繋がります。
系列、例えば2×7=14、2×8=16、2×9=18だから、かけられる数が1増える2×10=20というように、
2×10は、2に0を1つつければ良いんだよという教え方をするところもありますが、これでは倍概念は育ちません。
倍概念を理解してから、早く計算ができるために形式にもっていくことは、必ずしも良くないことではないですが、しっかり数量的に倍概念を教えることが大事です。その理解がわり算に繋がります。
かけ算の分解、穴あけをやらせる
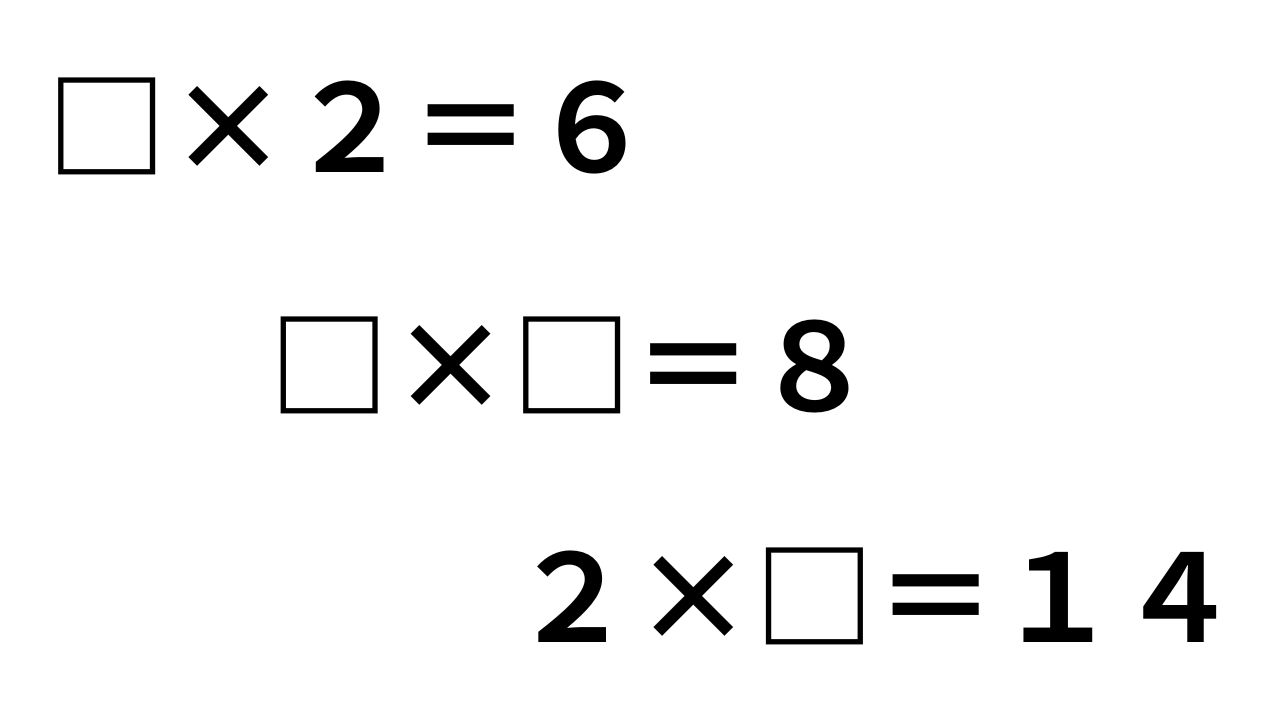
わり算の教えるポイント
2つめは、かけ算の穴あけをやらせるです。
意味づけかけ算を理解し九九を言えるようになったら、まずはバラバラで出題されている九九問題をやらせてください。
その問題を解く時に、注意することが1点。
それは、九九を1から唱えて答えをだしていないかです。
例えば、7×8=の問題があった時に、
7の段の1からつまり、7×1=7,7×2=14、7×3=21と順番に唱えてから7×8にたどり着いて答えをだしていないかです。
学習をスタートしたばかりで慣れるまでは仕方ないですが、ある程度の問題を解いたら、唱えなくても答えがでるようにすることが大事です。
そのためのステップとして、3段階が、
ステップ1
×1から順番に唱えて答えを出す
ステップ2
×5から順番に唱えて答えを出す(×5以上の場合)
ステップ3
唱えなくてもすぐに答えがでる
このステップ3までクリアしてから、かけ算の穴あけ問題をやらせます。
かけ算の穴あけ問題とは、
□×2=6、2×□=14
のようなかけられる数、かける数の部分を答えさせる問題です。
この問題がわり算の基礎になる大事な土台になります。
わり算の意味を教える
わり算の教えるポイント
3つ目は、わり算の意味を教えるです。
わり算の意味は2つ(等分除と包含除)があるから難しいと先ほどお話させていただきましたが、その意味を理解させることが重要です。
それには、実際の物を分けさせたり、絵を使って視覚で理解させることで意味が繋がります。
例えば
「等分除」
あめ12個用意し、3人で同じ数ずつ分けると伝えます。
3人にわける時に、1個ずつ配っていって最終的に4個ずつ分けられます。
それが、「等分除の意味」で1あたりの数をもとめるわり算になります。
等分除は、実際に物を使って操作をさせた方が、わかりやすく意味が理解できます。
その後、確かめさせることが大事です。
その確かめに先ほどポイントでお話した穴あけ問題を使います。
(式)12個÷3人=4個 ⇒□個×3人=12個(かけられる数が□) なので確かめは4×3=12
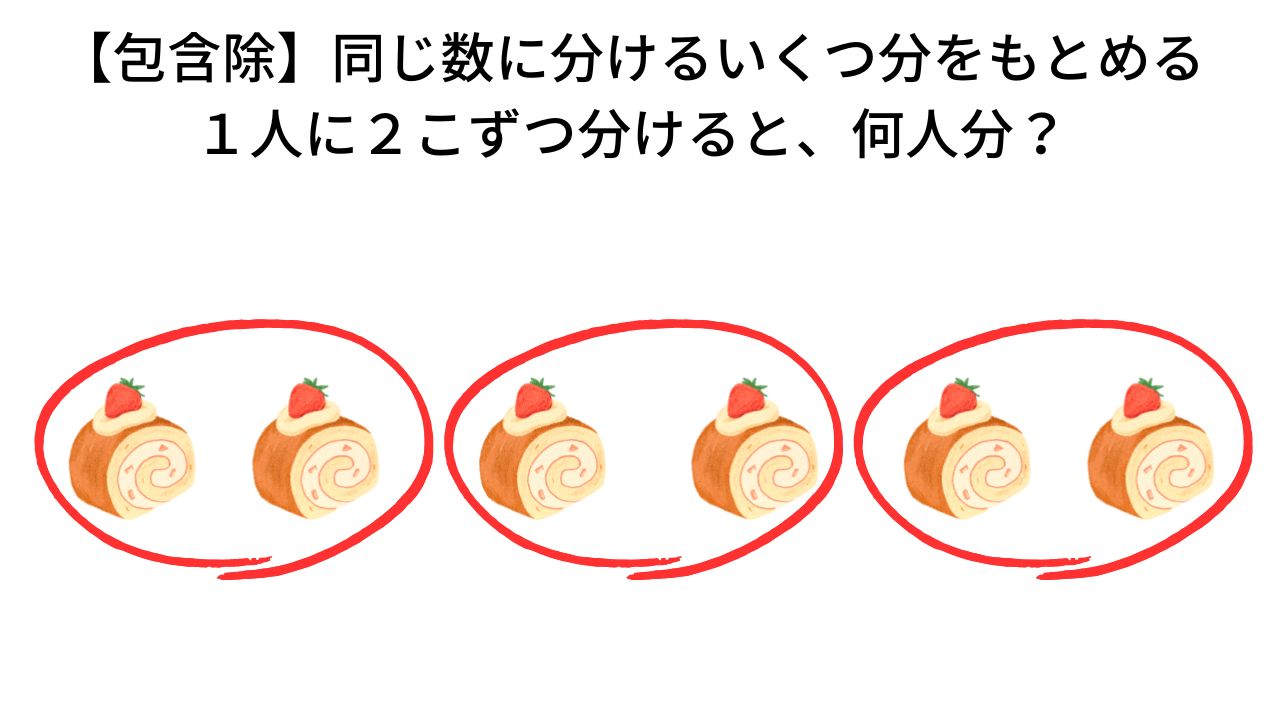
次に、「包含除」ですが、
こちらは絵を使って視覚で理解させる方がわかりやすいです。
あめ12個を描きます。3個ずつ配って、何人に配られるかという問題。
「3個ずつだから、3個〇でえんぴつで囲んで」と伝えます。
それが、「包含除の意味」で同じ数に分けるといくつ分をもとめるわり算になります。
つまり、12個の中に3がいくつ分入っているかということです。
確かめは、12個÷3個ずつ=4人 ⇒3個×□人=12個(かける数が□)なので確かめは3×4=12
答えを出させたら、確かめさせることが大事です。それがかけ算とわり算の関係性がわかり、わり算理解につながるからです。
あまりのあるわり算を絵を使って教える

わりきれるわり算ができたら、次にあまりがあるわり算です。
あまりがあるわり算を理解していないと、2桁3桁と数が大きくなった時にわからなくなってしまいます。
例えば、2桁のわり算だと、132÷2のように、初めに13÷2のあまりのあるわり算をもとめる問題のように、あまりのあるわり算が多いです。
それでは、どのようにあまりを教えたら良いのか、それは先に説明したように、実際の物を分けさせたり、絵を使って視覚で理解させることが大事です。
先ほどの例でお伝えしたあめの数を12個から13個に増やして、あまりがでる数でやらせます。
そして確かめが一番大事です。
13÷3=4あまり1⇒3×4+1=13
になりますね。
あまりのあるわり算は、視覚で1個あまっている。1個多いということを理解させることが大事です。
なので、1個多いから、あまりの分を+すれば確かめの式の答えがあうんだなと理解させます。
それが、桁の数が大きくなった時の計算の土台になります。
桁の大きい数のわり算を教える
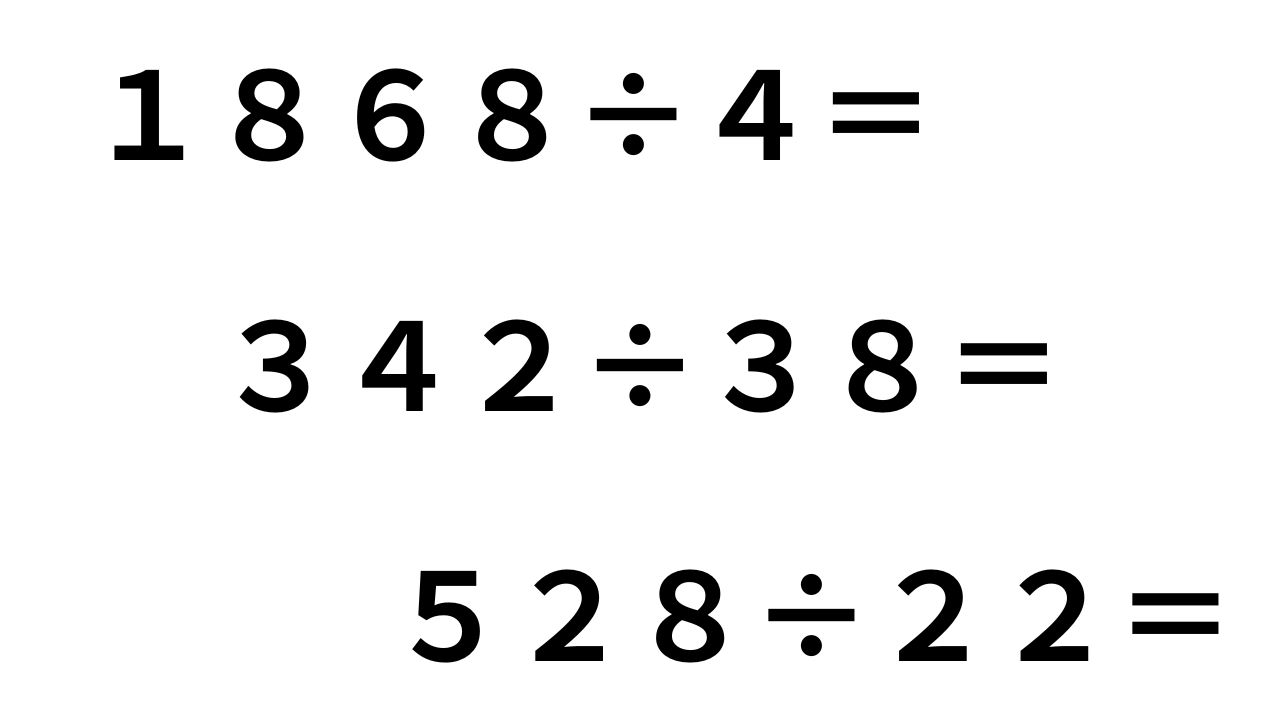
最後に大きな桁のわり算ですが、学年が上がるごとに大きな桁の計算になります。そのような中で、
4年生以降の高学年でわり算が苦手な子が結構います。
例えば、4年生で出題される問題は、342÷38=などのようにわる数が2桁になります。わる数も大きな桁になります。
わり算に苦手意識があるのに、学校で今習っているからと、無理やり大きな桁のわり算学習しても余計に苦手意識をもってしまいます。
まずは、時間がかかってしまいますが、
先ほどのわり算の教えるポイント
⑴かけ算の意味をしっかり理解しているか
⑵わり算とかけ算の穴あけ問題の確かめを理解しているか
⑶わり算の意味を理解しているか
⑷あまりのあるわり算ができるか
を理解させてから桁幅を少しずつ広げる計算をしていくことが大事です。
より分かりやすいわり算学習法
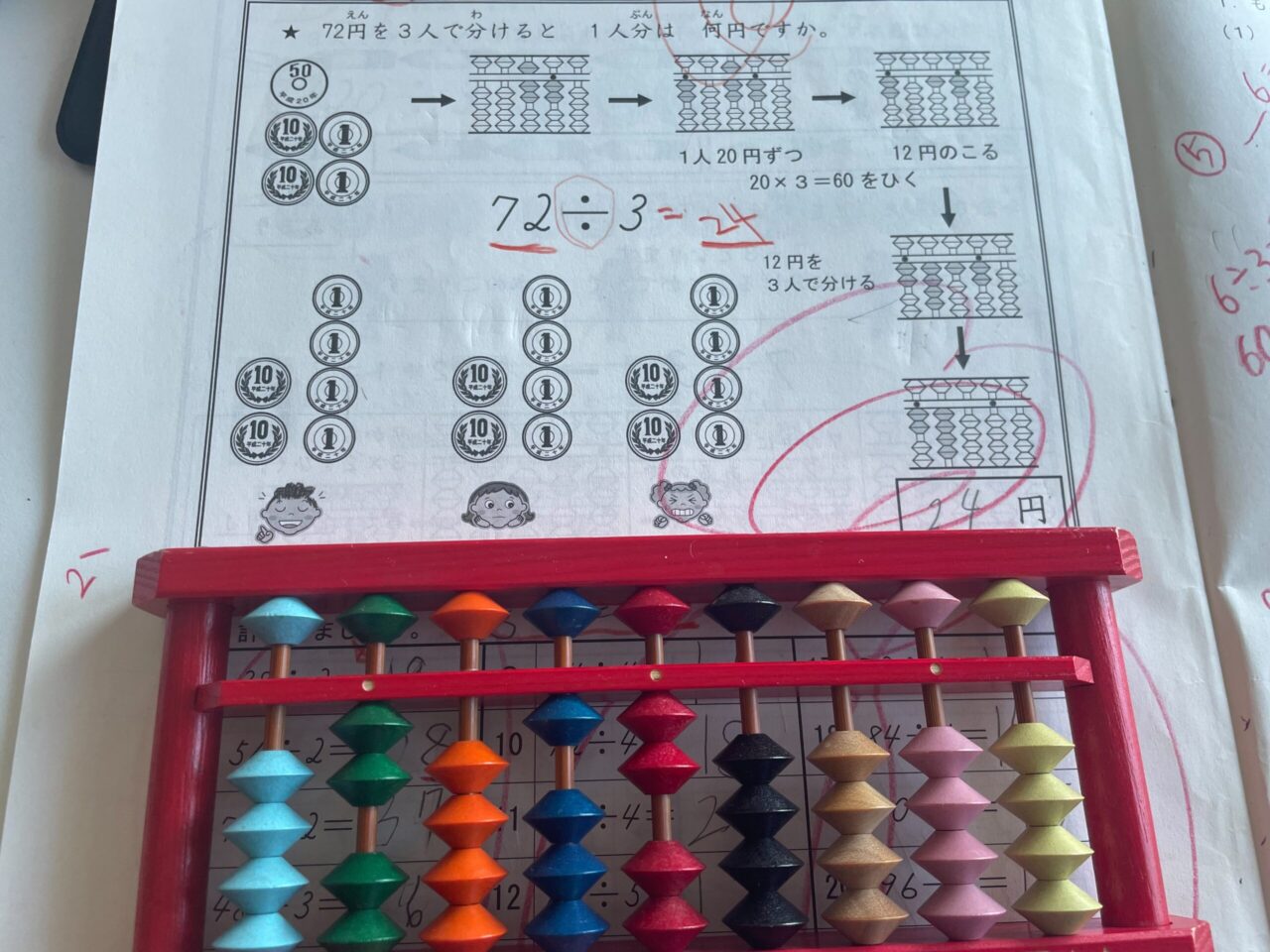
わかりやすいわり算学習法を最後にお伝えします。
それは、数の見える化できる教具+絵や文章問題で意味づけする学習です。
その数の見える化できる教具とは「そろばん」です。
そろばんは、計算の途中過程をみることができます。
例えば、132÷2の場合、商に60をたてた時に、60×2=120を引きます。残りが12と視覚でわかります。
残りの量がそろばん上に残っているのです。
それを利用して、テキストの文章問題や絵をあわせて学習することで、意味と結びつけわり算の仕組みを深く理解させることができます。
Q&A
Q.わり算が苦手な子にはどう教えたらいいですか?
わり算を教えるには、まずはかけ算の基礎をしっかり理解させることが大切です。九九をただ唱えられるだけでなく、その意味を理解させることで、応用力がつきます。さらに、実際の物を使って「等分除」や「包含除」の意味を視覚的に学ばせることも効果的です。
Q.わり算を学ぶ重要性とは何ですか?
わり算は、小数や分数、単位計算、割合といった数学の基礎になります。これを理解していないと、後々の計算でつまずく原因となります。日常生活でも、割引計算や単位あたりの量の把握など、頻繁に使われます。
Q.わり算が苦手な理由は何ですか?
わり算は、計算の順番がたし算やかけ算と異なり、右からではなく左から進めるため戸惑いやすいです。また、わり算のパターンはかけ算よりも多く、理解が不十分だと混乱しやすくなります。
Q.あまりのあるわり算はどう教えればいいですか?
実際の物や絵を使って視覚的に理解させると効果的です。例えば、あめを分ける例を使い、余ったものをどのように表現するか学ばせます。確かめとして「3×4+1=12」のように逆の計算をさせ、理解を深めます。
まとめ
この記事では、割り算についてご紹介しました。
①なぜわり算は難しいか…5つの理由
・組み合わせの量が多い
・すべて使っての計算
・計算順番が逆
・あまりがある
・意味が2通り
②わり算はなぜ大事か…2選
・分数・小数の土台になる
・日常生活でよく使う
③わり算教え方のポイント…5段階
・かけ算の意味をしっかりおしえる
・かけ算の分解、穴あけをやらせる
・わり算の意味を教える
・あまりのあるわり算を絵を使って教える
・桁の大きい数のわり算を教える
その他、より分かりやすいわり算学習法をご紹介しました。
最後に教える上で大事なことをお伝えいたします。
わり算苦手なのはしょうがないんだという気持ちで子どもに接してください。
わり算が難しい理由をお伝えしたように、子どもにとってわり算は難しいです。
心配になると子どもに「なんでできないのー」と怒ってしまうことがあります。怒られた子どもは、よりわり算に苦手意識をもち、教えられても頭に入らなくなってしまいます。
「苦手でもしょうがないんだ。ゆっくり理解させよう」と余裕をもって子どもに接することで、子どもにも安心感を与え、わり算の教えるポイントにそって教えることでわり算の理解につながります。
あせらずに、じっくり教えてくださいね。それが日常つかえるわり算に結びつきます。
🍀 無料プレゼントのお知らせ
もし、
✔ うちの子がどの段階で止まっているのか知りたい
✔ 家庭で何から始めればいいか迷っている
✔ 割り算の“どの部分”が弱いのか知りたい
と思われたら、
🎁 無料診断チェックシート(PDF) 🎁 割り算教える順序動画(期間限定視聴)
をLINEで受け取れます。
✔ 3分でつまずき原因が分かる
✔ 家庭での次の指導がわかる
✔ 子どもが混乱しにくい教え方が分かる
👇 無料診断・順序動画を受け取る(登録30秒)



